Riddler Answer:Fool the Bank

Put on your Hamburglar costumes, Riddler fans! This week’s puzzle takes a foray into racketeering by putting us in the shoes of an expert counterfeiter specializing in $100 bills. In one last hurrah, we need to optimize the number of fake bills to deposit alongside $2500 worth of real bills, knowing that the bank will randomly inspect 5% of them (rounded up) and have a 25% chance of detecting fake bill after inspecting it. Let’s do this thing…

Solution

To start, let’s define \(a\) as the portion of bills inspected, \(R\) as the number of real bills you deposit, and \(F\) as the number of fake bills you deposit. This would put the number of randomly inspected bills at

\[n = \text{ceil}(a(R + F)).\]

From here, we need to think about the probability (and therefore combinatorics) of how many fake/real bills the bank chose to inspect. If we set \(f\) as the number of fake bills the bank happens to scrutinize, the number of ways the bank could choose \(f\) fake bills and \(n\) bills total can be defined as

\[\Omega(f) = \frac{F!}{f!(F - f)!} \times \frac{R!}{(n - f)!(R - n + f)!}.\]

This would put the total number of inspection combinations at

\[Q = \sum_{f=0}^{n} \Omega(f).\]

Let’s also define \(p\) as the probability of a fake’s detection. To calculate the probability of success given that \(f\) fake bills were analyzed, we can normalize \(\Omega\) using \(Q\) and add a factor of \((1 - p)^{f}\) to account for the bank teller missing the fakes:

\[P(f) = \frac{\Omega(f)}{Q} (1 - p)^{f}.\]

Finally, we can sum this function over all possible values of \(f\) and multiply by the cash to be gained to get the expected return of our hypothetical caper:

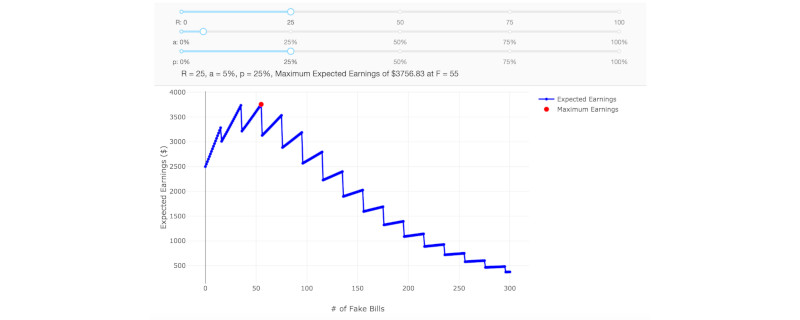
\[E(R,F) = 100(R + F)\sum_{f=0}^{n} P(f).\]

Using \(a = 0.05\), \(p = 0.25\), and \(R = 25\), we can vary \(F\) to produce a graph of expected return vs. number of fake bills. The maximum expected return occurs at \(F = 55\) with a 47.0% probability of winning $8000, suggesting an expected return of $3756.83.

Note: This post originally included an interactive widget that let you adjust the inspection rate, detection probability, and number of real bills to see how the optimal strategy changed. The widget has been retired, but the math and solution above remain valid.

The python code used to generate the values and figures above are available on my GitHub page.